Recently, I was invited to give a talk at the conference Automata Factory IV. While preparing the talk I was looking for a nice illustration of the talk content. Since the early days of the G-Art group, there were lots of exchanges about tilings, cellular automata and art. Many ideas started to emerge and their development is still ongoing. Finally, after some days, I came up with the following:
I love the result and in this post I would like to tell how it was produced. Indeed, the effect is produced by the ‘cooperation’ of three distinct ingredients: the father Truchet, an agents system and the artist Andy Warhol.



The cooperating artists (left to right): the father Truchet, an agent system and Andy Warhol.
Let us start from Truchet
Jean Truchet, also known under the name father Truchet was a famous scientist, mathematician and inventor who lived during the reign of the french king Louis XIV. Among other things he wrote an article published in the Histoire de l’académie royale des sciences (appeared on the January 1st, 1704) which can be considered one of the first systematic studies on tilings. In particular, he studied the tiling which nowadays is known as the Truchet tiling after him. This tiling is based on the following two tiles:


The round Truchet tiles: A (left) and B (right).
By combining the basic (round) tiles one can obtain an infinite number of nice tiling. The figure below provides a 3x3 example.
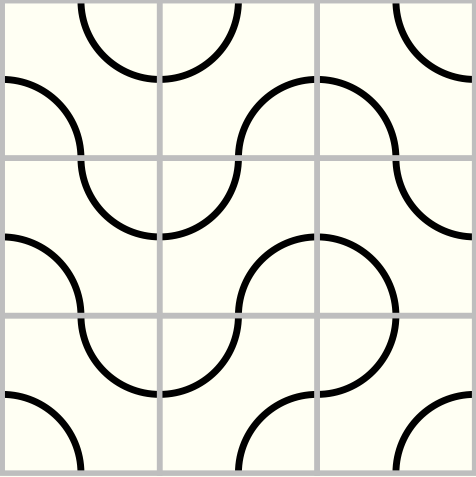
A 3x3 tiling based on Truchet round tiles.
Coloring the opposite corners of the tile in one color and the central part with another allows
to obtain very nice colorful tilings. The web is full of examples and some are even on sell (see
here for instance). We call stripe a connected
curve drawn connecting the round corners of the tiles. Stripes call for a series of puzzling questions.
We list here some of them (please let us know if some of them have already been answered):
- What is the probability that a stripe forms a closed curve? And how this probability is related to the size of the tiling?
- What is the probability that a n×n tiling contains closed curves only?
- How does it grow the length of longest stripe in a square tiling? (This one should be easier)
- …
Adding the agent system
On the top of each Truchet tile we are going to put two agents one per each corner stripe. Each agent can be in one of two states: healthy (blue) or ill (red). In this way we get 8 different tiles.
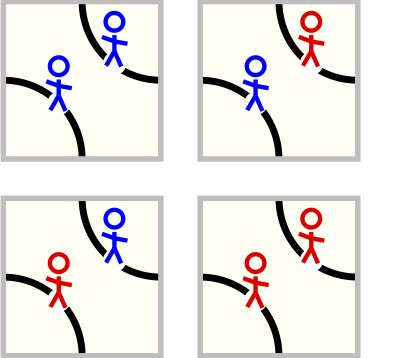
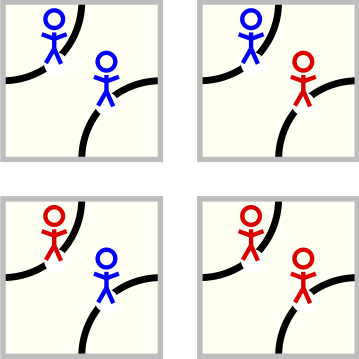
The Truchet tiles with the addition of the agents.
Consider a tiling made with this new set of tiles. At the beginning let all the agents be
in healthy state except for δ randomly extracted agents which are ill. At each iteration,
all agents will update their state according to their own state and to the one of their closest
neighbors along the same stripe. The update rule is very simple: an ill agent is ill forever; an healthy
agent become ill if one of its closest neighbors is ill.
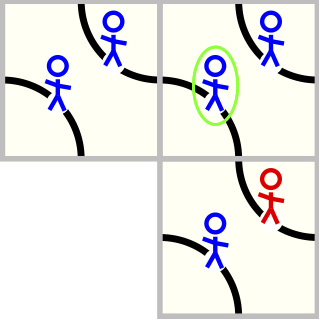

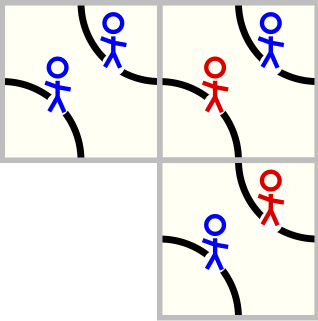
Updating an agent (green contour). If one of the neighbors on the same stripe is ill, then he gets ill. In this way the infection propagates.
More formally, if one represents the ill state by a 1 and the healthy state by a 0, then the update
rule of the agents is exactly the local rule of the elementary cellular automaton (ECA) with Wolfram
number 254. By exchanging the role of 1 and 0, this rule is essentially the same as ECA rule 128
which has been studied extensively in [1], for instance. This local rule can be written
as
f(x−1,x0,x+1)=x−1x0x+1
where x0 stand for the agent which is going to be updated (contoured in green in the
previous image), x−1 (resp. x+1) stands for its left (resp. right) neighbor
along the same stripe. Indeed, ECA rules 128 and 254 are elements of a larger class of CA, namely
freezing CA which was introduced in [2]. At this point another bunch of interesting
questions arises:
- Are all CA useful to produce diffusion effects like the one in the previous section freezing CA?
- Is the dynamics of freezing CA characterized by signal subshifts described in [1]?
- There are freezing CA with non-sofic limit set. Can we characterize the subclass of freezing CA with sofic limit set?
- How large is the previous subclass with respect to the class of freezing CA?
Last comes Warhol...
The last step of the realization is based on (a cropped version of) a famous portrait of Marylin Monroe by Andy Warhol. The idea is to color the portion of stripe on which an ill agent is positioned in red, while all of the rest of the tiling will become transparent.

Using the underlying tiling to filter image pixels. Only the stripes (or portion of stripes) populated with ill agents is used in the filtering process.
Finally, the obtained picture will be used as a filters on the Marylin picture to extract only the pixels found on a red stripe. Taking one snapshot per iteration and assembling them with some specific software produces the movie that we have seen at the beginning.
Of course, at this point more questions arise:
- What is the best ratio between the size of a tile and the size of the original image?
- What is the best choice for the background color? Indeed, a too clear (white) background tends to fade the overall image, while a dark one will increase too much the contrast.
- What is the best compromise between number of agents, diffusion rate and respawn rate?
We are pretty proud of the overall effect obtained both the artistic production and for getting
a new interesting bunch of scientific question to investigate. We hope you love them as well.
We are currently working for answering some of those questions.
References
[1] Enrico Formenti and Petr Kurka. Subshift attractors of cellular automata. Nonlinearity, 20:105-117, 2007.
[2] Eric Goles, Nicolas Ollinger, Guillaume Theyssier, Introducing Freezing Cellular Automata, in: AUTOMATA 2015, Vol. 24 of TUCS Lecture Notes, Turku, Finland, 2015, pp. 65–73.
Credits: The picture of father Truchet was taken from Wikipedia and it is in the public domain. The picture
of Andy Warhol is taken from Fondation Louis Vitton website.

